You and Your R - Doing Statistics in Python
In this post, I will tell you how to do statistics in Python. I’ve been trained in statistics mostly with R, but I do a lot of fMRI analyses in Python and do not really want to switch back and forth.
Table of Contents
- Table of Contents
- Intro
- Prepare dataset
- Correlation
- One-sample t-test
- Independent sample t-test
- OLS Regression
- ANOVA
- Generalized Linear Models
- Linear Mixed Effects
Intro
We will be using several Python’s modules such as numpy, scipy and statsmodels. Numpy and scipy are standard modules. Statsmodels are shipped with anaconda, but if you somehow do not have statsmodels, install them via pip install -U statsmodels or easy_install -U statsmodels. Good news is that statsmodels allow doing statistics with R-like formulas (most of the time)!
In R we often work with dataframes. In Python, the dataframes are handled with Pandas, which by the way works fine with missing values. In case you do not have it, install it! Hint: pip install pandas should work ;)
Here is a very nice tutorial on Pandas, which I have no intention to rewrite here. It explains how to handle data in timeseries, dataframes, subsetting data, reading and writing, and many more.
Prepare dataset
#set common stuff
%matplotlib inline
import pandas as pd
import numpy as np
import scipy as sp
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
np.set_printoptions(threshold='nan') #to print the whole array
Here I will make up a dataset. I will use two continuous variables, as well as one variable that good for nesting and one binary variable. To make sense out of it, here are the names for these variables. One continuous variable will be liking ice cream (just because I love it!) on a scale from 0 to 100 (hate to love respectively). It may be our dependent variable. The other continuous variable: the temperature of the weather, nesting variable is for the cities where the data were collected, and the last binary variable is for having kids. Please keep in mind, I’m not going to decipher what each model told us about the variables or whether it makes sense to run them together in a model. My goal is to show that we can run a variety of models in python, and the results will be identical to an output from R.
#generate correlated data
xx = np.array([-30.0, 110.0])
yy = np.array([0., 1000.0])
means = [xx.mean(), yy.mean()]
stds = [xx.std() / 10, yy.std() / 10]
corr = 0.7 # correlation
covs = [[stds[0]**2 , stds[0]*stds[1]*corr],
[stds[0]*stds[1]*corr, stds[1]**2]]
m = np.random.multivariate_normal(means, covs, 2500).T
plt.scatter(m[0], m[1])
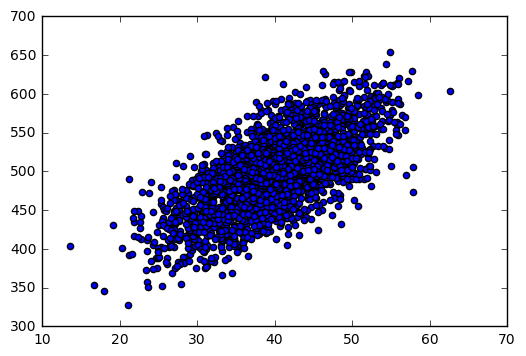
# categorical variable
cities = np.random.randint(0, 50, 2500,dtype='i')
# binary variable
kids = np.random.randint(0, 2, 2500,dtype='i')
# Convert to Pandas. Here to make sense of all the models below, I made up some variable names.
df = pd.DataFrame({'ice_cream':m[1], 'temp': m[0], 'cities': cities, 'kids': kids})
# Assuming different cities have different preferences
for num in xrange(50):
df['ice_cream'][df['cities']==num] += df['temp']*num
# Assuming liking ice cream is increased with kids (1; no kids = 0)
df['ice_cream'][df['kids']==1] += df['temp']*1.5
# scale
df['ice_cream'] = df['ice_cream']/35
# Here is how to plot the df
df.plot(x='temp', y='ice_cream', kind='scatter', c='cities', ax=None, subplots=False, sharex=None, sharey=False,
layout=None, figsize=None, use_index=True, title='DF', grid=None, legend=True, style=None,
logx=False, logy=False, loglog=False, xticks=None, yticks=None, xlim=None, ylim=None, rot=None,
fontsize=None, colormap=None, table=False, yerr=None, xerr=None, secondary_y=False, sort_columns=False)
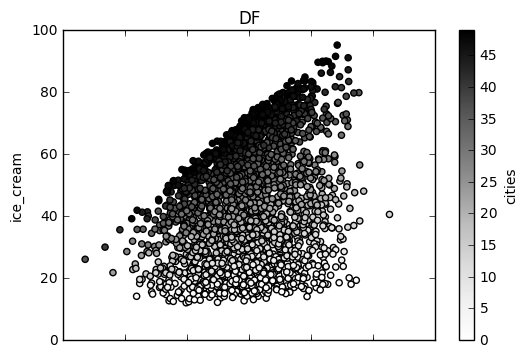
#Preview the top few lines
df.head()
| cities | ice_cream | kids | temp | |
|---|---|---|---|---|
| 0 | 19 | 47.529669 | 1 | 57.004601 |
| 1 | 42 | 67.420913 | 0 | 42.419001 |
| 2 | 42 | 61.912708 | 0 | 39.236830 |
| 3 | 32 | 50.251380 | 1 | 38.797294 |
| 4 | 16 | 34.368304 | 1 | 41.432471 |
# Summary
df.describe()
| cities | ice_cream | kids | temp | |
|---|---|---|---|---|
| count | 2500.000000 | 2500.000000 | 2500.00000 | 2500.000000 |
| mean | 24.492000 | 42.867872 | 0.48960 | 39.899549 |
| std | 14.563366 | 17.665057 | 0.49999 | 6.889043 |
| min | 0.000000 | 12.006117 | 0.00000 | 13.531745 |
| 25% | 12.000000 | 27.950608 | 0.00000 | 35.380744 |
| 50% | 24.000000 | 41.268259 | 0.00000 | 39.998665 |
| 75% | 38.000000 | 56.383082 | 1.00000 | 44.571119 |
| max | 49.000000 | 95.132215 | 1.00000 | 62.615418 |
# save it for replications in R
df.to_csv("~/exchange.csv")
Correlation
print "Pearson correlation with Pandas"
df.corr(method='pearson') #also available ‘kendall’ and ‘spearman’
Pearson correlation with Pandas
| cities | ice_cream | kids | temp | |
|---|---|---|---|---|
| cities | 1.000000 | 0.926675 | -0.016553 | -0.044868 |
| ice_cream | 0.926675 | 1.000000 | 0.034269 | 0.288360 |
| kids | -0.016553 | 0.034269 | 1.000000 | -0.017963 |
| temp | -0.044868 | 0.288360 | -0.017963 | 1.000000 |
print "Pearson correlation with Numpy"
print np.corrcoef(df['ice_cream'],df['temp'])
Pearson correlation with Numpy
[[ 1. 0.28836048]
[ 0.28836048 1. ]]
print "Pearson correlation with Scipy"
r, p = sp.stats.pearsonr(df['ice_cream'],df['temp'])
print "correlation coefficient: ", r, "; p-value: ", p
Pearson correlation with Scipy
correlation coefficient: 0.28836047698 ; p-value: 4.47496022458e-49
Looks like Scipy is the only way to test for significance
# Replicate in R
cities 1.00000000 0.92667534 -0.01655296 -0.04486818
ice_cream 0.92667534 1.00000000 0.03426892 0.28836048
kids -0.01655296 0.03426892 1.00000000 -0.01796342
temp -0.04486818 0.28836048 -0.01796342 1.00000000
One-sample t-test
We’ll be using the same dataframe from above.
# Using scipy
t, p = sp.stats.ttest_1samp(df['ice_cream'], popmean=0)
print "t-value: ", t, "; p-value: ", p
t-value: 121.335222203 ; p-value: 0.0
# Replicate in R
One Sample t-test
data: df$ice_cream
t = 121.34, df = 2499, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
42.17508 43.56067
sample estimates:
mean of x
42.86787
Independent sample t-test
# With scipy
t, p = sp.stats.ttest_ind(df['ice_cream'],df['temp'])
print "t-value: ", t, "; p-value: ", p
t-value: 7.82751207811 ; p-value: 6.03132649935e-15
# With statsmodels that also give degrees of freedom
t, p, df = sm.stats.ttest_ind(df['ice_cream'],df['temp'])
print "t-value: ", t, "; p-value: ", p, "; df: ", df
t-value: 7.82751207811 ; p-value: 6.03132649935e-15 ; df: 4998.0
# Statsmodels with an unequal variance that is a default in R
# Using numpy arrays since df gives an error
t, p, df = sm.stats.ttest_ind(np.asarray(df['ice_cream']),np.asarray(df['temp']),
alternative='two-sided', usevar='unequal')
# alternative also accepts 'larger' and 'smaller' as one-sided indications
print "t-value: ", t, "; p-value: ", p, "; df: ", df
t-value: 7.82751207811 ; p-value: 6.68488304875e-15 ; df: 3241.93905035
# Replicate in R
Welch Two Sample t-test
data: df$ice_cream and df$temp
t = 7.8275, df = 3241.9, p-value = 6.685e-15
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
2.224794 3.711851
sample estimates:
mean of x mean of y
42.86787 39.89955
OLS Regression
# Finally using an R-like formula :)
lm = smf.ols('ice_cream ~ temp',data=df).fit()
print lm.summary()
OLS Regression Results
==============================================================================
Dep. Variable: ice_cream R-squared: 0.083
Model: OLS Adj. R-squared: 0.083
Method: Least Squares F-statistic: 226.6
Date: Tue, 25 Oct 2016 Prob (F-statistic): 4.47e-49
Time: 13:12:17 Log-Likelihood: -10617.
No. Observations: 2500 AIC: 2.124e+04
Df Residuals: 2498 BIC: 2.125e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 13.3653 1.989 6.719 0.000 9.465 17.266
temp 0.7394 0.049 15.052 0.000 0.643 0.836
==============================================================================
Omnibus: 599.927 Durbin-Watson: 2.017
Prob(Omnibus): 0.000 Jarque-Bera (JB): 108.273
Skew: 0.056 Prob(JB): 3.08e-24
Kurtosis: 1.987 Cond. No. 238.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Replicate in R
Call:
lm(formula = ice_cream ~ temp, data = df)
Residuals:
Min 1Q Median 3Q Max
-37.10 -14.21 -0.45 14.40 41.70
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.36530 1.98908 6.719 2.25e-11 ***
temp 0.73942 0.04913 15.052 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 16.92 on 2498 degrees of freedom
Multiple R-squared: 0.08315, Adjusted R-squared: 0.08278
F-statistic: 226.6 on 1 and 2498 DF, p-value: < 2.2e-16
#Now using kids as a factor in an interaction
lm2 = smf.ols('ice_cream ~ temp * C(kids)',data=df).fit()
print lm2.summary()
OLS Regression Results
==============================================================================
Dep. Variable: ice_cream R-squared: 0.087
Model: OLS Adj. R-squared: 0.086
Method: Least Squares F-statistic: 79.05
Date: Tue, 25 Oct 2016 Prob (F-statistic): 7.53e-49
Time: 13:15:08 Log-Likelihood: -10612.
No. Observations: 2500 AIC: 2.123e+04
Df Residuals: 2496 BIC: 2.126e+04
Df Model: 3
Covariance Type: nonrobust
=====================================================================================
coef std err t P>|t| [95.0% Conf. Int.]
-------------------------------------------------------------------------------------
Intercept 17.2132 2.800 6.147 0.000 11.722 22.705
C(kids)[T.1] -7.8929 3.972 -1.987 0.047 -15.683 -0.103
temp 0.6262 0.069 9.080 0.000 0.491 0.761
temp:C(kids)[T.1] 0.2328 0.098 2.372 0.018 0.040 0.425
==============================================================================
Omnibus: 606.961 Durbin-Watson: 2.011
Prob(Omnibus): 0.000 Jarque-Bera (JB): 108.752
Skew: 0.057 Prob(JB): 2.43e-24
Kurtosis: 1.985 Cond. No. 619.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Replicate in R
Call:
lm(formula = ice_cream ~ temp * kids, data = df)
Residuals:
Min 1Q Median 3Q Max
-37.481 -14.184 -0.603 14.247 40.521
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17.21324 2.80043 6.147 9.19e-10 ***
temp 0.62622 0.06897 9.080 < 2e-16 ***
kids1 -7.89288 3.97245 -1.987 0.0470 *
temp:kids1 0.23279 0.09812 2.372 0.0177 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 16.89 on 2496 degrees of freedom
Multiple R-squared: 0.08677, Adjusted R-squared: 0.08567
F-statistic: 79.05 on 3 and 2496 DF, p-value: < 2.2e-16
More info http://statsmodels.sourceforge.net/stable/examples/notebooks/generated/ols.html
ANOVA
table = sm.stats.anova_lm(lm, typ=2) # Type 2 ANOVA DataFrame
print table
sum_sq df F PR(>F)
temp 64843.702800 1.0 226.551244 4.474960e-49
Residual 714979.828862 2498.0 NaN NaN
# Replicate in R
Df Sum Sq Mean Sq F value Pr(>F)
temp 1 64844 64844 226.6 <2e-16 ***
Residuals 2498 714980 286
Generalized Linear Models
mod1 = smf.glm('kids ~ ice_cream', data=df, family=sm.families.Binomial()).fit()
print mod1.summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: kids No. Observations: 2500
Model: GLM Df Residuals: 2498
Model Family: Binomial Df Model: 1
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -1730.9
Date: Tue, 25 Oct 2016 Deviance: 3461.7
Time: 13:36:46 Pearson chi2: 2.50e+03
No. Iterations: 6
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -0.2081 0.105 -1.979 0.048 -0.414 -0.002
ice_cream 0.0039 0.002 1.713 0.087 -0.001 0.008
==============================================================================
# Replicate in R
Call:
glm(formula = kids ~ ice_cream, family = "binomial", data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.241 -1.157 -1.114 1.195 1.246
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.208145 0.105173 -1.979 0.0478 *
ice_cream 0.003884 0.002268 1.713 0.0868 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 3464.7 on 2499 degrees of freedom
Residual deviance: 3461.7 on 2498 degrees of freedom
AIC: 3465.7
Number of Fisher Scoring iterations: 3
More info: http://statsmodels.sourceforge.net/stable/glm.html and http://statsmodels.sourceforge.net/devel/contrasts.html
Linear Mixed Effects
# Cold ratings are nested into brands, there is only one random slople - intercept
model1 = sm.MixedLM.from_formula("ice_cream ~ temp", data=df, groups=df["cities"]).fit(reml=False)
print model1.summary()
Mixed Linear Model Regression Results
========================================================
Model: MixedLM Dependent Variable: ice_cream
No. Observations: 2500 Method: ML
No. Groups: 50 Scale: 10.0311
Min. group size: 38 Likelihood: -6609.5008
Max. group size: 70 Converged: Yes
Mean group size: 50.0
--------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
--------------------------------------------------------
Intercept 8.921 2.360 3.780 0.000 4.296 13.547
temp 0.851 0.009 91.185 0.000 0.833 0.869
Intercept RE 271.356 17.322
========================================================
# Replicate in R
Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: ice_cream ~ temp + (1 | cities)
Data: df
AIC BIC logLik deviance df.resid
13227.0 13250.3 -6609.5 13219.0 2496
Scaled residuals:
Min 1Q Median 3Q Max
-4.5515 -0.5695 -0.0070 0.5589 3.7772
Random effects:
Groups Name Variance Std.Dev.
cities (Intercept) 271.35 16.473
Residual 10.03 3.167
Number of obs: 2500, groups: cities, 50
Fixed effects:
Estimate Std. Error t value
(Intercept) 8.921509 2.360016 3.78
temp 0.851126 0.009334 91.19
Correlation of Fixed Effects:
(Intr)
temp -0.158
model2 = sm.MixedLM.from_formula("ice_cream ~ temp", data=df, re_formula="temp", groups=df["cities"]).fit(reml=False)
print model2.summary()
Mixed Linear Model Regression Results
=================================================================
Model: MixedLM Dependent Variable: ice_cream
No. Observations: 2500 Method: ML
No. Groups: 50 Scale: 1.8684
Min. group size: 38 Likelihood: -4551.3137
Max. group size: 70 Converged: Yes
Mean group size: 50.0
-----------------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------------
Intercept 8.599 0.173 49.774 0.000 8.261 8.938
temp 0.862 0.060 14.433 0.000 0.745 0.980
Intercept RE 0.151 0.412
Intercept RE x temp RE -0.164 0.073
temp RE 0.178 0.026
=================================================================
# Replicate in R
Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: ice_cream ~ temp + (1 + temp | cities)
Data: df
AIC BIC logLik deviance df.resid
9114.6 9149.6 -4551.3 9102.6 2494
Scaled residuals:
Min 1Q Median 3Q Max
-3.06647 -0.72209 0.01464 0.71654 2.74365
Random effects:
Groups Name Variance Std.Dev. Corr
cities (Intercept) 0.1505 0.3879
temp 0.1777 0.4216 -1.00
Residual 1.8684 1.3669
Number of obs: 2500, groups: cities, 50
Fixed effects:
Estimate Std. Error t value
(Intercept) 8.59958 0.17196 50.01
temp 0.86235 0.05976 14.43
Correlation of Fixed Effects:
(Intr)
temp -0.381
More info: http://statsmodels.sourceforge.net/stable/mixed_linear.html
Please email me your comments and questions!
